De troposfeer
Bij straalverbindingen gaat het in principe om zeer gerichte verbindingen tussen twee punten. Vooral waar die commercieel worden aangeboden moet een bepaalde zekerheid worden gegarandeerd. Het is daar, maar ook voor amateurs, belangrijk te weten welke factoren bij deze verbindingen een rol spelen.
Straalverbindingen lopen normaal gesproken in hun geheel door de troposfeer, de onderste luchtlaag in de atmosfeer, waarin zich allerlei weersverschijnselen afspelen, maar er geen ionisatie is.
Een straalverbinding wordt beïnvloed door de eigenschappen van en veranderingen in de troposfeer, zoals:
- brekingsindex;
- meerwegfading (vaak frequentieselectief);
- grondreflecties;
- scintillatie;
- demping door verschillende gassen;
- regendemping.
Breking en buiging
Om de voortplantingsrichting van een elektromagnetische golf in de troposfeer te bepalen moet eerst worden onderzocht wat er gebeurt als een elektromagnetische golf een grensvlak tussen twee media met verschillende dichtheden passeert.
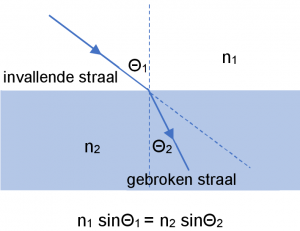
Als de dichtheid van medium 2 groter is dan de dichtheid van medium 1 zal de doorgaande golf worden verbogen zoals in de figuur. Als medium 2 minder dicht zou zijn dan medium 1, zou de golf juist de andere kant op gebroken worden. Het verband tussen de hoeken x en x” wordt gegeven door de wet van Snellius.
De brekingsindex van elk medium heeft een rechtstreeks verband met de voortplantingssnelheid van de golf in dat medium.
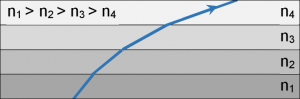
De troposfeer kan worden voorgesteld door zeer veel schillen in lagen op elkaar die ieder een gebied markeren met een verschillende brekingsindex. Een radiogolf zou bij iedere overgang een kleine breking ondergaan. In werkelijkheid is het verloop in dichtheid continu, en een golf ondergaat in de troposfeer een continue buiging.
Onder normale omstandigheden neemt de brekingsindex af bij toenemende hoogte, hetgeen betekent dat de elektromagnetische golven, in plaats van zich rechtlijnig voort te planten, afbuigen in de richting van de aarde.
De volgende factoren hebben invloed op de brekingsindex:
- luchtdruk (mb);
- absolute temperatuur (in Kelvin);
- waterdampdruk (mb).
Omdat breking veroorzaakt wordt door verschillen in de brekingsindex, en buiging dus door het verloop in de brekingsindex, is het belangrijk inzicht te verkrijgen in dat verloop als functie van de hoogte. Hiervoor zijn drie jaar lang metingen gedaan, waarvan de volgende tabel de meetresultaten aangeven voor de eerste 150 meter boven het aardoppervlak. Zonder verder te wiskundig te willen worden, moeten we nog weten dat de letter N de brekingsindex aangeeft, en de uitdrukking dN/dH het verloop hiervan met de hoogte. Een minteken wil zeggen dat N bij toenemende hoogte afneemt.
[dN/dH] (N/km)
10% 50% 90%
Jaar −68 −41 −22
Winter −56 −37 −22
Lente −74 −42 −24
Zomer −77 −46 −24
Herfst −63 −40 −18
In de tabel zien we dat, over het hele jaar genomen, dN/dH even vaak (50% van de tijd) lager is dan −41, als hoger. Slechts 10% van de tijd is deze waarde kleiner dan −68, en ook slechts 10% van de tijd is hij hoger dan −22: volgens de tabel is hij immers 90% van de tijd lager dan dat getal. Uit de metingen bleek eveneens (niet in de tabel opgenomen) dat voor 1% van de tijd dN/dH onder −113 ligt, en ook 1% van de tijd boven +8. En de in die drie jaar eenmalig gemeten extreme waarden waren −237 en +129. Door de buiging verwijdert de radiogolf zich niet zo snel van het aardoppervlak als bij zuiver rechtlijnige voortplanting het geval zou zijn. De reikwijdte wordt er dus door vergroot. Bij het ontwerpen van straalverbindingen is de bolvorm van de aarde belangrijk, en er wordt dus vaak met de straal van de aarde gerekend. Die is ca. 6370 km, maar door de buiging lijkt het voor de golf alsof de aarde ‘minder bol’ is, dus alsof de aardstraal groter is. Deze schijnbare verandering van de straal van de aarde geven we aan met de factor K.
Uit de tabel blijkt ook dat de ‘gemiddelde waarde’ (de jaarlijkse mediaan) van dN/dH in de buurt van de −40 ligt. Voor deze waarde is K= 1,33
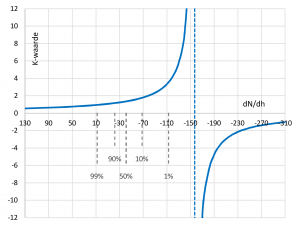
In de afbeelding is K als functie van dN/dH weergegeven. Onderaan in de grafiek staan de resultaten uit de tabel. Inderdaad lezen we horizontaal bij 50% af dat dN/dH= −40, en verticaal dat de bijbehorende K ca. 1,33 is.
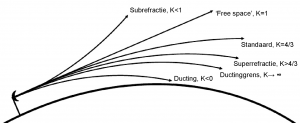
Een bijzonder waarde is dN/dH= −157. Voor deze waarde wordt K ‘oneindig’, hetgeen betekent dat de schijnbare aardstraal oneindig wordt: voor de golven lijkt de aarde nu gehaal plat. Wat er gebeurt, is dat bij deze waarde voor dN/dH de elektromagnetische golven precies de kromming van de aarde volgen. Een waarde van K=1 zou betekenen dat de golven zich rechtlijnig voortplanten en dus niet buigen. En voor waarden van K kleiner dan 1 buigen de elektromagnetische golven zich niet naar de aarde toe, maar juist ervan af.
Meerwegfading
Nu hoeft dN/dH niet op elke hoogte gelijk te zijn, of zelfs maar geleidelijk te verlopen. En afhankelijk van het verloop van de dN/dH als functie van de hoogte is het mogelijk dat de elektromagnetische golven via diverse verschillende wegen door de troposfeer de ontvangstantenne bereiken. Deze golven hebben, door de verschillende voortplantingssnelheden en afgelegde afstanden, verschillende fasen en amplitudes ten opzichte van elkaar. Ze kunnen daardoor leiden tot zowel versterking als verzwakking van het ontvangstniveau. Dit verschijnsel staat bekend als meerwegfading.
Andere vormen van fading
Wateroppervlakken. Een opmerkelijke vorm van fading, die in de inleiding al genoemd is, treedt op bij trajecten die een reflectiepunt hebben waarvoor geldt dat de reflectiecoëfficiënt ongeveer −1 is (bijvoorbeeld trajecten over water). De gereflecteerde golf interfereert met de directe golf en is praktisch even sterk. De signaalsterkte kan daardoor zeer laag worden, zelfs – of juist – op een verbinding die praktisch ‘zicht’ is. Het weglengteverschil tussen de rechtstreekse en de gereflecteerde golf bedraagt dan precies een oneven aantal halve golflengten. Bij signalen met een relatief breed frequentiespectrum, ATV of sommige digitale datamodes, betekent dit dat bepaalde frequenties veel meer gedempt worden dan andere frequenties uit het spectrum; we hebben dan dus frequentieselectieve fading.
Scintillatie
Er kan ook sprake zijn van een situatie waarin de directe elektromagnetische golf juist een veel grotere amplitude heeft dan alle andere golven die de ontvangstantenne via verschillende wegen bereiken. Aan de ontvangstkant wordt dan een veldsterkte gemeten die snel en licht fluctueert met een gaussische verdeling. Dit verschijnsel noemt men scintillatie (‘fonkelen’: het licht van sterren, gezien door de atmosfeer, doet dit ook, door dezelfde oorzaak).
Demping door gassen
De elektromagnetische golven van een straalverbinding worden gedempt door moleculaire absorptie door zuurstof en waterdamp. Voor veel frequenties speelt dit een ondergeschikte rol, maar op 22 GHz is de demping door zuurstof 0,1 dB/km, en door waterdamp 0,16 dB/km.
Regendemping
Regen veroorzaakt eveneens absorptie (dus demping). Maar naast absorptie veroorzaakt regen ook verstrooiing van de elektromagnetische golven. De grootste intensiteit van regen treedt slechts op langs een beperkt gedeelte van het straalverbindingstraject. Bij het berekenen van de ‘beschikbaarheid’ wordt met dit verschijnsel rekening gehouden door een correctiefactor in te voeren die een functie is van de trajectafstand. In Nederland geldt volgens de geraadpleegde tekst dat gedurende 0,01% van de tijd de regenintensiteit groter is dan 22 mm/uur.
Path clearance, obstakels
Behalve de bolle aarde zelf, kunnen ook andere obstakels een straalverbinding hinderen; denk aan bergen, maar ook aan hoge gebouwen. Om hieraan te rekenen moeten we echter wat dieper in de natuurkunde duiken, waarbij we het ‘beginsel van Huygens’ en de theorie van Fresnel nodig hebben. Hierover is meer geschreven in Electron van april 2018.
Voor formules en theoretische onderbouwing, zie o.a. RECOMMENDATION ITU-R P.530-8